Maximal torus

In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.

A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G (and therefore isomorphic to the standard torus Tⁿ). A maximal torus is one which is maximal among such subgroups. That is, T is a maximal torus if for any other torus T′ containing T we have T = T′. Every torus is contained in a maximal torus simply by dimensional considerations. A noncompact Lie group need not have any nontrivial tori (e.g. Rⁿ).

The dimension of a maximal torus in G is called the rank of G. The rank is well-defined since all maximal tori turn out to be conjugate. For semisimple groups the rank is equal to the number of nodes in the associated Dynkin diagram.

1 Examples
2 Properties
3 Weyl group
4 See also

Examples

The unitary group U(n) has as a maximal torus the subgroup of all diagonal matrices. That is,

$T = \left\{\mathrm{diag}(e^{i\theta_1},e^{i\theta_2},\dots,e^{i\theta_n})�: \forall j, \theta_j \in \mathbb R\right\}.$

T is clearly isomorphic to the product of n circles, so the unitary group U(n) has rank n. A maximal torus in the special unitary group SU(n) ⊂ U(n) is just the intersection of T and SU(n) which is a torus of dimension n − 1.

A maximal torus in special orthogonal group SO(2n) is a given by the set of all simultaneous rotations in n pairwise orthogonal 2-planes. This is also a maximal torus in the group SO(2n+1) where the action fixes the remaining direction. Therefore, both SO(2n) and SO(2n+1) have rank n. For example, in the rotation group SO(3) the maximal tori are given by rotations about a fixed axis.

The symplectic group Sp(n) has rank n. A maximal torus is given by the set of all diagonal matrices whose entries all lie in a fixed complex subalgebra of H.

Properties

Let G be a compact, connected Lie group and let 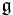$\mathfrak g$ be the Lie algebra of G.

A maximal torus in G is a maximal abelian subgroup, but the converse need not hold.
The maximal tori in G are exactly the Lie subgroups corresponding to the maximal abelian, diagonally acting subalgebras of 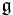$\mathfrak g$ (cf. Cartan subalgebra)
Given a maximal torus T in G, every element g ∈ G is conjugate to an element in T.
Since the conjugate of a maximal torus is a maximal torus, every element of G lies in some maximal torus.
All maximal tori in G are conjugate. Therefore, the maximal tori form a single conjugacy class among the subgroups of G.
It follows that the dimensions of all maximal tori are the same. This dimension is the rank of G.
If G has dimension n and rank r then n − r is even.

Weyl group

Given a torus T (not necessarily maximal), the Weyl group of G with respect to T can be defined as the normalizer of T modulo the centralizer of T. That is, 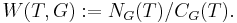$W(T,G)�:= N_G(T)/C_G(T).$ Fix a maximal torus 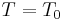$T = T_0$ in G; then the corresponding Weyl group is called the Weyl group of G (it depends up to isomorphism on the choice of T). The representation theory of G is essentially determined by T and W.

The Weyl group acts by (outer) automorphisms on T (and its Lie algebra).
The centralizer of T in G is equal to T, so the Weyl group is equal to N(T)/T.
The identity component of the normalizer of T is also equal T. The Weyl group is therefore equal to the component group of N(T).
The normalizer of T is closed, so the Weyl group is finite
Two elements in T are conjugate if and only if they are conjugate by an element of W. That is, the conjugacy classes of G intersect T in a Weyl orbit.
The space of conjugacy classes in G is diffeomorphic to the orbit space T/W.

Maximal torus

Contents

Examples

Properties

Weyl group

See also